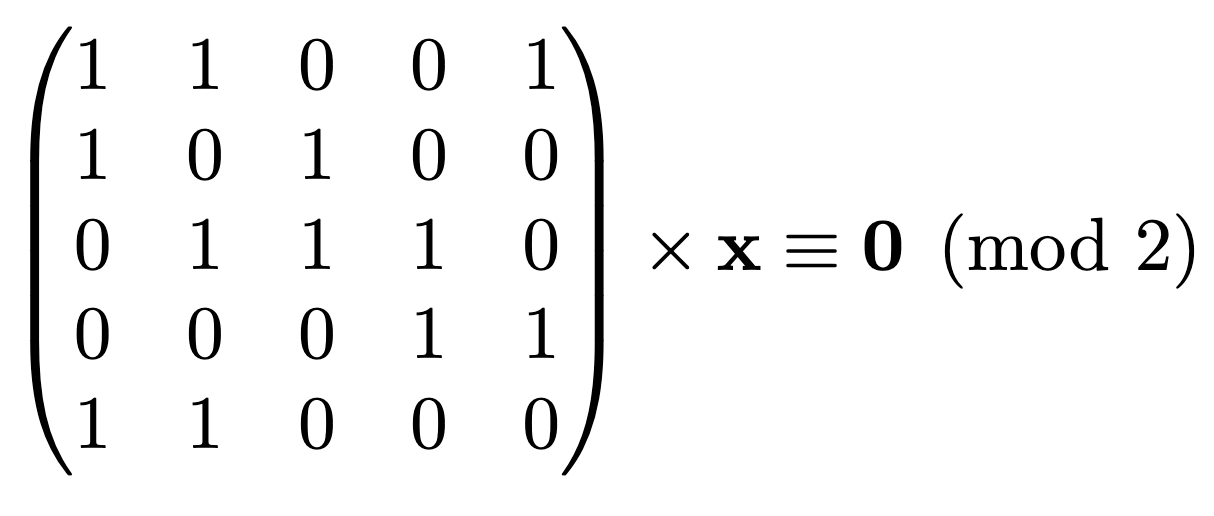Quadratic Sieve

Python / Number Theory / Cryptography

Implementation Details

The algorithm begins by determining a smoothness bound B using the heuristic exp(sqrt(ln(n)*ln(ln(n)))/2). We construct a factor base of prime numbers where the Legendre symbol (n/p) equals 1. To efficiently identify smooth numbers, we solve the modular square root congruence for each prime in the base using the Tonelli-Shanks algorithm. These roots define the starting offsets for our sieve.

Algorithm Pseudocode — Fig 1. Formal definition of the Quadratic Sieve factorization implemented in Python. \(S[i]\) denotes the accumulated log-sum at index \(i\) of the sieve array, used to identify smooth numbers. The final step computes the GCD using the constructed congruence \(X^2 \equiv Y^2 \pmod n\), where \(sqrt(\prod x_i^2)\) is the product of the collected roots (\(X\)) and \(sqrt(\prod Q(x_i))\) is the square root of the product of the B-smooth numbers (\(Y\)).

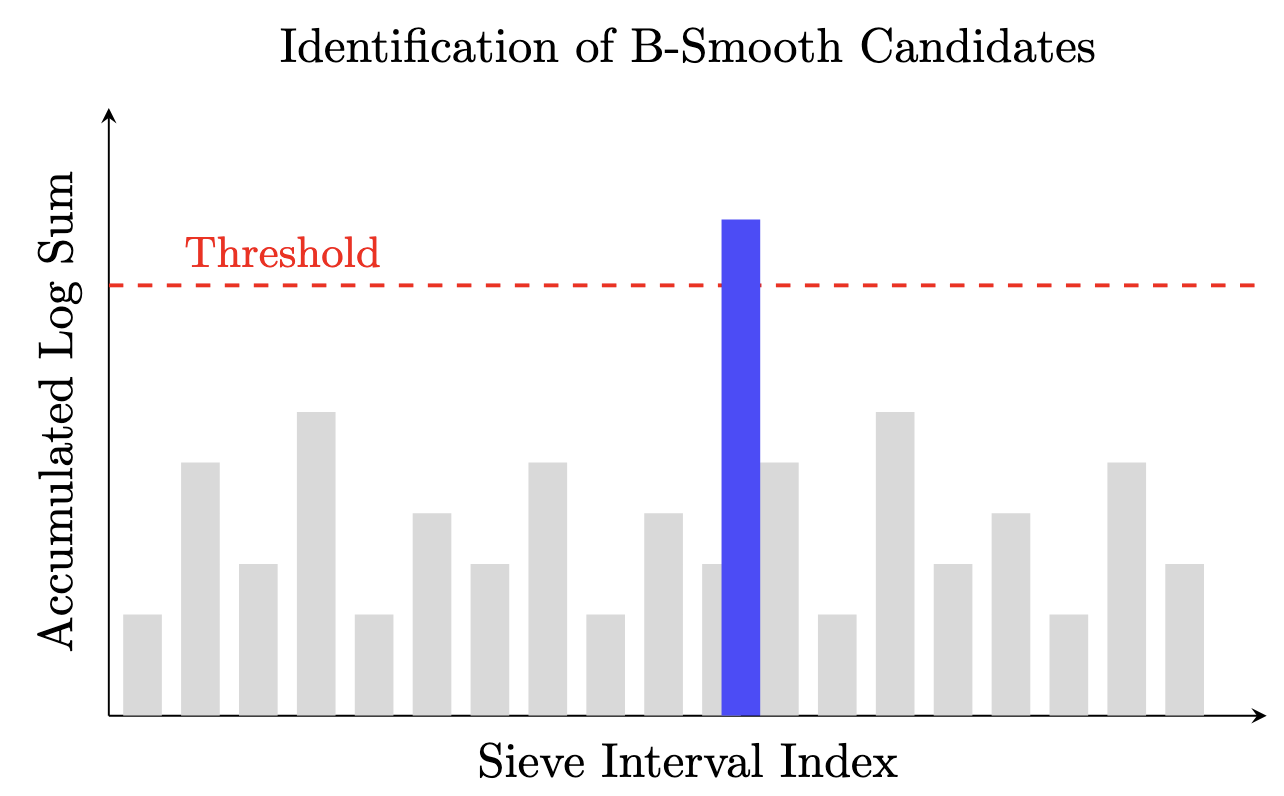
We initialize a sieve array over an interval and add the logarithm of p to indices corresponding to the arithmetic progressions of the roots. Indices where the accumulated log-sum exceeds a threshold are flagged as candidate B-smooth numbers.

Log-Sum Visualization — Fig 2. Visualization of the sieving interval. The red line represents the target threshold derived from the polynomial. Indices where the accumulated log sum exceeds this threshold (blue bar) are flagged as candidate smooth numbers.

We verify these candidates via trial division and collect their exponent vectors. Once the number of relations exceeds the size of the factor base, we form a matrix of exponent parities. We perform Gaussian elimination over the field GF(2) to find the null space. Each vector in the kernel corresponds to a subset of relations whose product is a perfect square. This yields a congruence of squares, allowing us to compute the greatest common divisor to reveal the non-trivial prime factors.

GF(2) Matrix Reduction — Fig 3. The linear algebra part, solving for the null space of the exponent matrix (mod 2) to find a linear dependency, identifying the perfect square required to factor the composite number.